Trois problèmes ouverts du routage météorologique en marine marchande
Scénarios climatologiques, calibration spectrale et instabilité des trajectoires optimales
Capitaine illimité de la marine marchande — SL Mar – Marine Consultancy
Correspondance : [email protected]
Cet article identifie trois problèmes fondamentaux du routage météorologique en marine marchande et propose des approches pour chacun. Il s’inscrit dans le cadre de recherche du projet WindMar et définit la feuille de route théorique pour les versions futures du système.
Résumé
L’optimisation de routes météorologiques en marine marchande repose sur trois hypothèses rarement questionnées : que les prévisions météorologiques constituent une entrée suffisante pour l’optimisation, que le modèle de performance du navire est fiable, et que l’espace des trajectoires possibles admet une structure exploitable par les méthodes d’optimisation classiques. Cet article montre que ces trois hypothèses sont problématiques et propose des approches pour chacune.
Le premier problème — l’inadéquation des prévisions climatologiques génériques — est traité par la sélection d’analogues historiques dans les réanalyses ERA5, mesurés par distance de Wasserstein spatio-temporelle et organisés par clustering en scénarios physiquement cohérents, puis explorés par simulations de Monte Carlo paramétriques conditionnelles pour produire des distributions de consommation.
Le deuxième — l’écart entre le modèle hydrodynamique et le comportement réel du navire — est traité par la reconstitution du spectre directionnel de vagues en route, dont les descripteurs calibrent les paramètres de résistance ajoutée et de perte de vitesse.
Le troisième — l’instabilité des solutions dans l’espace des trajectoires stochastiques — est traité par une paramétrisation des routes en courbes spline contraintes dans un couloir à décroissance exponentielle.
L’objectif n’est pas d’automatiser la décision de route, mais de fournir aux navigateurs les outils d’analyse nécessaires pour qu’ils effectuent eux-mêmes des arbitrages éclairés.
Mots-clés : routage météorologique, distance de Wasserstein, ensembles analogues, Monte Carlo paramétrique, spectre de vagues, calibration hydrodynamique, splines contraintes, aide à la décision maritime.
1. Introduction
Le routage météorologique promet des économies de carburant de l’ordre de 3 à 5 % en moyenne pour la marine marchande [1, 3], avec des cas pouvant atteindre 7 à 10 % dans des conditions favorables. Ces chiffres, cohérents entre les études académiques et les analyses de flotte [2], justifient l’intérêt croissant des armateurs et des régulateurs pour ces systèmes, en particulier dans le contexte des indicateurs CII et EEXI.
Cependant, la pratique opérationnelle du routage révèle trois problèmes fondamentaux que les systèmes commerciaux ne traitent pas — ou traitent implicitement, sans en exposer les conséquences. Ces trois problèmes concernent respectivement l’entrée météorologique, le modèle de performance du navire et la structure de l’espace d’optimisation.
Le premier problème est celui de la pertinence des scénarios météorologiques utilisés. Les systèmes actuels fonctionnent soit sur une prévision déterministe unique, soit sur les membres d’un ensemble numérique (ECMWF ENS, GEFS). Dans le premier cas, on optimise sur un scénario qui ne se réalisera pas. Dans le second, les membres sont trop peu nombreux (31 à 51) pour estimer les queues de distribution, et ne garantissent pas la cohérence physique entre variables. Dans les deux cas, l’optimiseur travaille avec une représentation pauvre de l’espace des situations météorologiques possibles.
Le deuxième problème est celui de la fidélité du modèle navire. Les courbes de résistance ajoutée et de perte de vitesse en vagues sont issues de formulations semi-empiriques (Stawave, Liu–Papanikolaou) calibrées sur des conditions idéalisées. En conditions réelles — houle croisée, spectre multi-pic, fouling, conditions de chargement variables —, l’écart modèle–réalité peut atteindre le même ordre de grandeur que le gain attendu du routage. Pour réduire cet écart, il faut injecter dans le modèle le spectre de mer réellement rencontré, ce qui suppose de le reconstituer à partir des mesures disponibles à bord.
Le troisième problème est celui de la structure de l’espace d’optimisation. L’espace des trajectoires stochastiques — l’ensemble des chemins possibles dans un champ de coûts aléatoire — est dépourvu de structure régulière. Une optimisation multi-objectif de type Pareto dans cet espace produit des fronts fragmentés et des sauts topologiques entre solutions voisines, incompatibles avec l’exploitation opérationnelle.
Le présent article analyse ces trois problèmes et propose pour chacun une approche : la sélection d’analogues météorologiques par distance de Wasserstein et clustering (problème 1), la calibration du modèle hydrodynamique par reconstitution spectrale (problème 2), et la paramétrisation des routes par splines contraintes à enveloppe exponentielle (problème 3). L’objectif n’est pas de construire un système de routage automatique, mais de fournir aux marins les moyens d’analyse poussés pour qu’ils réalisent eux-mêmes les arbitrages.
1.1 État actuel de l’implémentation (WindMar v0.0.6)
Les approches proposées dans cet article constituent une feuille de route théorique. Le système WindMar, dans sa version actuelle (v0.0.6), implémente un pipeline opérationnel qui couvre déjà une partie de la chaîne, mais avec des méthodes plus simples que celles proposées ici. Il est important de situer précisément ce qui existe pour comprendre ce que les trois problèmes ouverts ajouteraient.
| Axe | Cet article propose | WindMar v0.0.6 implémente |
|---|---|---|
| Scénarios météo (problème 1) |
Sélection d’analogues ERA5 par distance de Wasserstein spatio-temporelle, clustering en 3–5 scénarios nommés, Monte Carlo conditionnel (N = 1 000–10 000) | Prévision déterministe unique (NOAA GFS 0,25°, 5 jours), pré-ingérée dans PostgreSQL sur un cycle de 6 heures. Simulation de Monte Carlo paramétrique (N = 100) avec perturbations corrélées temporellement (décomposition de Cholesky), mais appliquées autour de la prévision GFS unique — pas de recherche d’analogues, pas de clustering |
| Modèle navire (problème 2) |
Reconstitution du spectre directionnel \(S(f, \theta)\) à partir de capteurs embarqués, calibration des paramètres de résistance par partition spectrale | Modèle Holtrop–Mennen avec paramètres scalaires d’état de mer (\(H_s\), \(T_p\), direction) issus des grilles de prévision. Calibration par moindres carrés non linéaires (scipy) à partir de rapports de midi (noon reports). Pas de reconstitution spectrale |
| Trajectoires (problème 3) |
Paramétrisation par B-splines cubiques (\(N_c\) = 4–8 points de contrôle) dans un couloir à décroissance exponentielle \(\Delta_0 e^{-t/\tau}\), avec ré-optimisation MPC | Recherche A* sur grille océanique 8-connectée (résolution 0,5°), lissage Douglas-Peucker + filtre d’angle de giration (< 15°). Deux stratégies de vitesse présentées après optimisation (« Same Speed » / « Match ETA »). Pas de paramétrisation spline, pas de couloir contraint |
Les deux captures d’écran ci-dessous illustrent l’état actuel du système. La route originale (tracé bleu) et la route optimisée par A* (tracé vert pointillé) sont affichées simultanément sur la carte. Le panneau de comparaison (en bas à gauche) présente deux onglets de stratégie de vitesse — « Same Speed » et « Match ETA » — avec les économies de carburant et de temps associées.
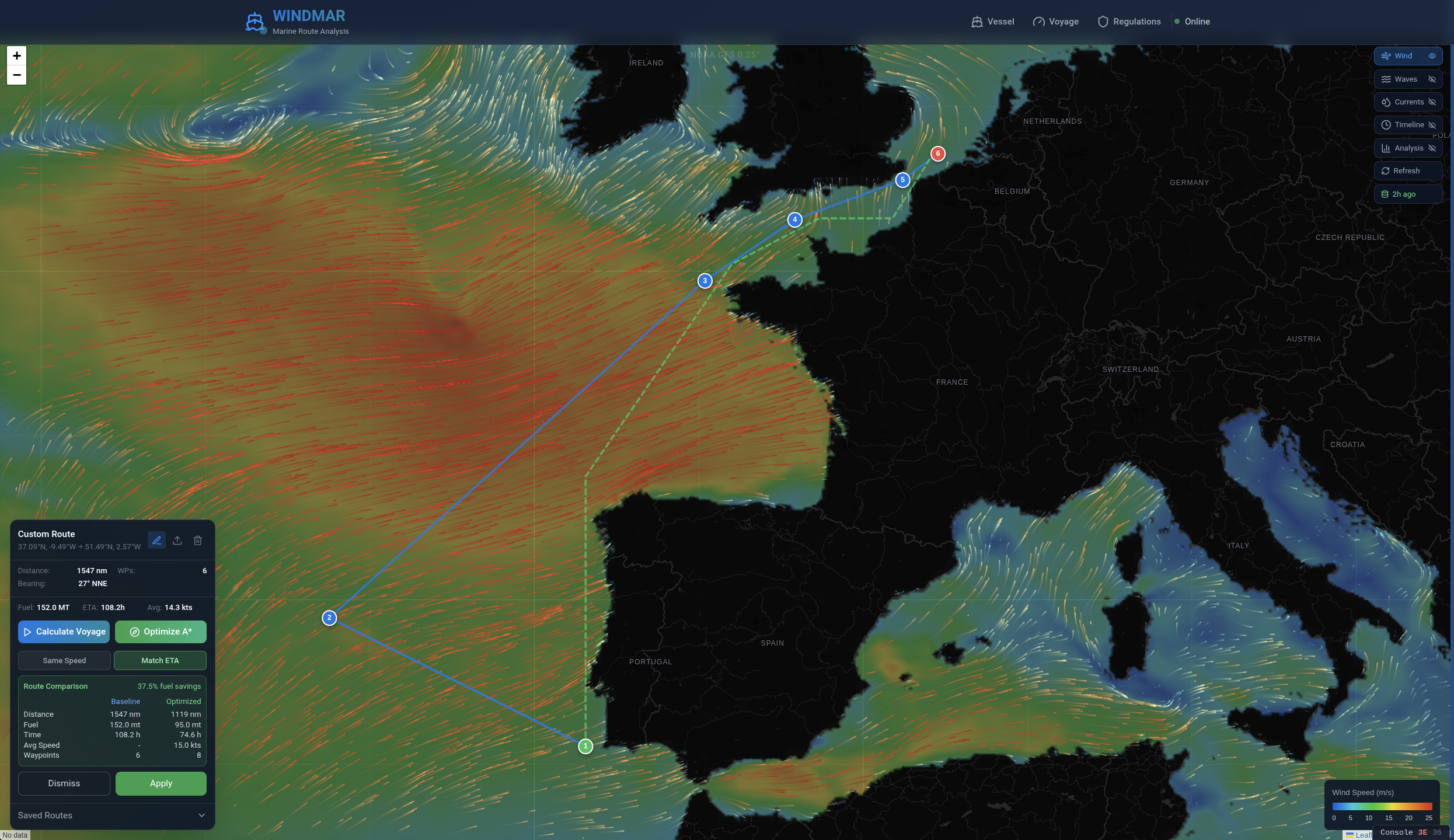
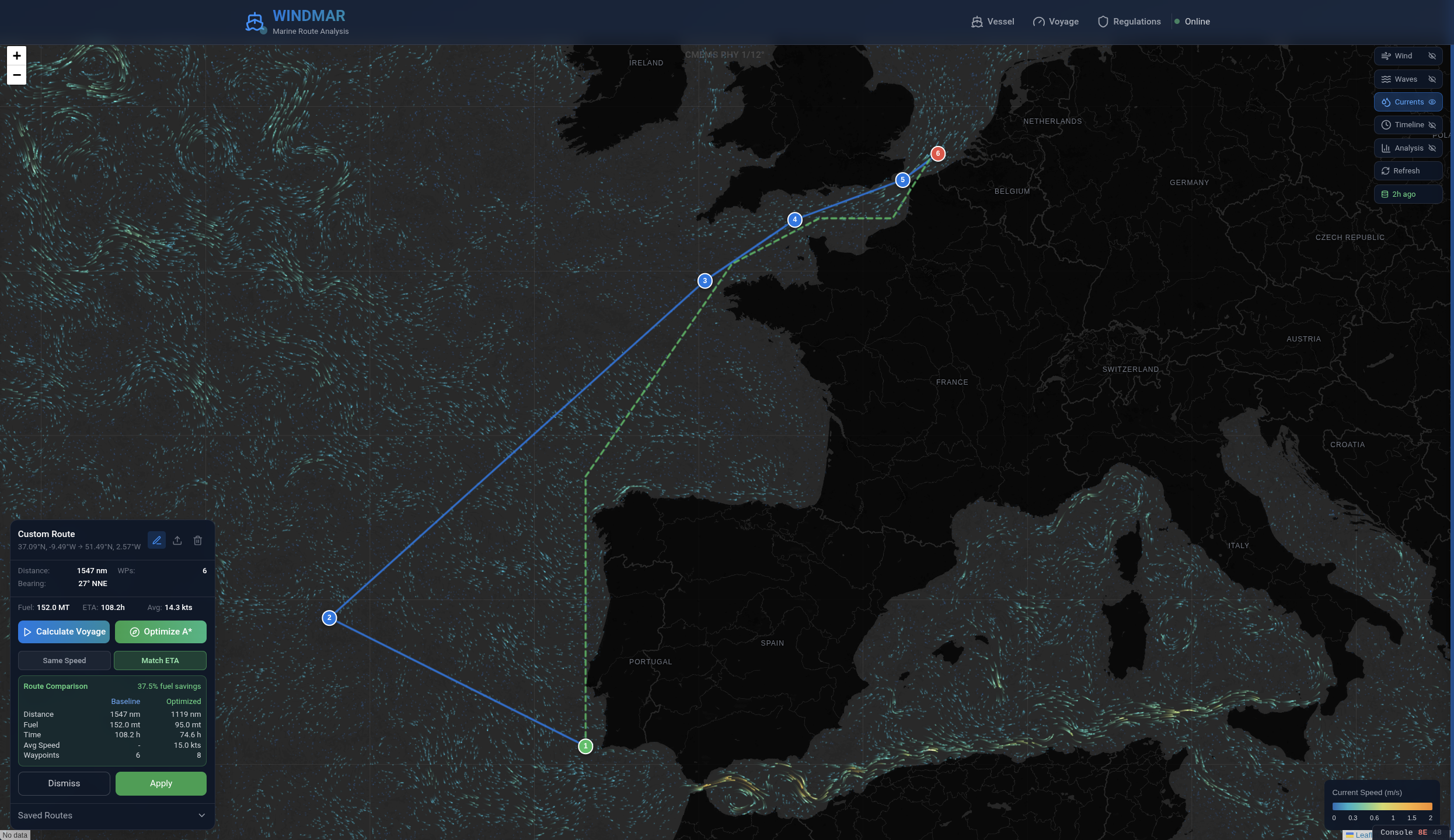
Le système actuel fournit donc un routage A* fonctionnel avec météo temporelle, un modèle de performance calibrable, et une quantification d’incertitude par Monte Carlo — mais sur une seule prévision, avec des paramètres scalaires de mer, et dans un espace de trajectoires non structuré. Les trois problèmes ouverts identifiés ci-dessous visent à lever ces trois limitations.
2. Problème 1 : l’inadéquation des scénarios météorologiques
2.1 Diagnostic
Le routage météorologique classique utilise une prévision déterministe comme entrée. Cette prévision est fiable 3 à 5 jours pour les champs synoptiques [4], alors qu’une traversée transocéanique dure 10 à 20 jours. Au-delà de l’horizon fiable, l’optimiseur exploite des gradients qui ne se matérialiseront pas.
L’alternative — utiliser les ensembles numériques (ECMWF ENS à 51 membres, GEFS à 31 membres) — ne résout pas le problème. Ces ensembles sont conçus pour caractériser l’incertitude atmosphérique globale, non pour fournir des scénarios exploitables au niveau d’une route maritime. Leurs membres ne sont pas indépendants, leur nombre est insuffisant pour estimer les queues de distribution, et ils ne garantissent pas la cohérence physique entre les variables (un membre peut présenter un vent fort avec une mer plate, combinaison qui n’existe pas dans la réalité).
Une troisième approche consiste à échantillonner des scénarios à partir de distributions paramétriques ajustées sur la climatologie (Weibull pour le vent, Rayleigh pour \(H_s\), Von Mises pour les directions). Mais cette approche produit des réalisations statistiquement plausibles et météorologiquement incohérentes : les corrélations spatio-temporelles entre variables ne sont pas capturées par des distributions marginales, même couplées par une matrice de corrélation.
Toutes ces approches traitent la météo comme un bruit à caractériser statistiquement, alors qu’elle est un ensemble de situations à identifier.
2.2 Approche proposée : ensembles analogues et distance de Wasserstein
Nous proposons de remplacer l’échantillonnage paramétrique par une recherche d’analogues historiques dans les réanalyses ERA5 [9]. Le principe est simple : plutôt que de générer des scénarios synthétiques, on recherche dans 84 ans de données (1940–2024) les situations réelles qui ressemblent à la prévision courante.
Chaque analogue est physiquement cohérent par construction : il s’est réellement produit. Les corrélations spatio-temporelles entre vent, vagues, courant et pression sont capturées implicitement, sans modélisation explicite. La méthode des ensembles analogues (AnEn) est établie en prévision météorologique [12] ; son application au routage maritime, combinée à une métrique de similarité adaptée, constitue l’originalité de cette proposition.
2.2.1 Pourquoi la similarité spatio-temporelle est essentielle
Un analogue doit correspondre non seulement à l’état métocéanique moyen, mais aussi à la géographie et à la dynamique temporelle de la situation. Une dépression de 3 m de \(H_s\) dans l’océan Indien n’a rien en commun avec une dépression de même amplitude en Atlantique Nord : le fetch, les courants, la bathymétrie et le régime synoptique sont entièrement différents. De même, une mer de 3 m qui monte n’est pas équivalente à une mer de 3 m qui descend : la première annonce une détérioration, la seconde une amélioration.
La similarité doit donc être mesurée sur une fenêtre spatio-temporelle : typiquement une zone de 200×200 milles nautiques sur 24 à 48 heures, qui capture la structure spatiale et l’évolution de la situation.
2.2.2 Choix de la distance de Wasserstein
La distance de Wasserstein (ou Earth Mover’s Distance) [10] mesure le coût de transport optimal pour transformer une distribution empirique en une autre. Une fenêtre météo constitue un nuage de points dans l’espace \((H_s, T_p, u_{\text{vent}}, v_{\text{vent}}, p_{\text{atm}})\) ; un analogue ERA5 constitue un autre nuage de points. La distance de Wasserstein quantifie combien de « masse » il faut déplacer pour transformer l’un en l’autre.
Son avantage décisif est la tolérance aux décalages spatiaux : un champ de pression décalé de 50 milles produit une erreur euclidienne importante alors que le patron météorologique est identique, simplement déplacé. La distance de Wasserstein capte cette proximité structurelle. La distance de Mahalanobis suppose des distributions gaussiennes, hypothèse discutable pour \(H_s\) et pour les directions circulaires. Le Dynamic Time Warping gère les décalages temporels mais est unidimensionnel.
Les variables angulaires sont transformées via \(\theta \to (\cos\theta, \sin\theta)\). Le coût de calcul, en \(O(n^3)\) exact, est ramené à un niveau tractable par les solveurs régularisés (Sinkhorn-Knopp) [11] après pré-filtrage géographique et saisonnier.
2.2.3 Pipeline de sélection et clustering
La sélection procède en quatre étapes :
| Étape | Méthode | Réduction |
|---|---|---|
| 1. Pré-filtrage | Masque par zone géographique et saison (±1 mois) | ~750 000 → ~60 000 |
| 2. Criblage rapide | Distance euclidienne sur les scalaires moyennés (\(H_s\) moyen, vent moyen, pression moyenne) | ~60 000 → ~500 |
| 3. Classement fin | Distance de Wasserstein sur les distributions multivariées spatio-temporelles complètes | ~500 → K = 50–100 |
| 4. Clustering | Regroupement des K analogues en familles de scénarios (k-means ou HDBSCAN) | K → 3–5 scénarios |
Chaque cluster représente un type d’évolution météorologique : « dépression passant au nord », « dépression passant au sud », « anticyclone persistant », etc. Les clusters sont pondérés par fréquence historique, ajustée par proximité Wasserstein à la prévision courante.
Le navigateur ne reçoit plus une prévision unique, mais une carte de 3 à 5 situations plausibles, identifiées, nommables et compréhensibles, chacune assortie d’une probabilité.
2.2.4 Simulations de Monte Carlo paramétriques conditionnelles
Le clustering fournit la structure ; il reste à explorer la variabilité intra-scénario. Pour chaque cluster, les distributions des variables métocéaniques sont ajustées paramétriquement — Weibull pour la vitesse du vent, Rayleigh pour \(H_s\), Von Mises pour les directions — conditionnellement au scénario identifié. On échantillonne ensuite des milliers de réalisations (\(N\) = 1 000 à 10 000) à l’intérieur de chaque cluster.
Cette approche combine les avantages des deux mondes :
- Les analogues fournissent la cohérence physique inter-variables et la structure spatio-temporelle : les corrélations vent–vagues–courant–pression sont celles de situations réelles, pas d’un modèle de corrélation.
- Le paramétrique fournit la puissance d’échantillonnage nécessaire pour estimer les queues de distribution et les intervalles de confiance, ce que 50 à 100 analogues seuls ne permettent pas.
Chaque réalisation Monte Carlo est propagée à travers le modèle de performance calibré (section 3) pour produire une estimation de consommation. Le résultat, par scénario, n’est pas un chiffre mais une distribution : « 430–460 t à 90 % de confiance » plutôt que « 452 t ».
3. Problème 2 : la calibration du modèle hydrodynamique par reconstitution spectrale
3.1 Diagnostic
Les modèles de résistance ajoutée en vagues — Stawave-1/2 [8], Liu–Papanikolaou [6], formulations issues de Holtrop–Mennen [7] — prédisent la perte de vitesse et la surconsommation en fonction de paramètres scalaires d’état de mer : hauteur significative \(H_s\), période pic \(T_p\), direction moyenne de la houle. Ces modèles sont calibrés sur des essais en bassin ou des campagnes de mesure en conditions contrôlées.
En exploitation réelle, l’écart entre ces prédictions et le comportement observé du navire peut être considérable, pour deux raisons.
D’abord, les paramètres scalaires ne décrivent pas la mer. Un spectre à deux pics (houle longue de secteur + mer du vent de travers), fréquent dans l’Atlantique, produit des sollicitations très différentes d’un spectre unimodal de même \(H_s\) : les phénomènes de roulis paramétrique, de slamming ou de résonance dépendent de la structure spectrale, pas de ses moyennes.
Ensuite, les conditions du navire en exploitation s’écartent des conditions d’essai : fouling biologique [5], tirant d’eau et assiette variables, vieillissement mécanique. L’erreur cumulée — simplification spectrale plus écart état du navire — peut atteindre plusieurs pourcents de la consommation, soit l’ordre de grandeur du gain attendu du routage.
3.2 Approche proposée : reconstitution spectrale et calibration
Pour réduire cet écart, nous proposons d’utiliser le spectre directionnel de vagues reconstruit à partir des mesures disponibles à bord — accéléromètres, inclinomètres, éventuellement radar bande X (type Wavex/Miros) — pour calibrer en continu les paramètres du modèle hydrodynamique.
3.2.1 Du spectre aux descripteurs
Le spectre directionnel \(S(f, \theta)\) est projeté sur un ensemble de descripteurs qui caractérisent l’état de mer de manière plus riche que les seuls scalaires \((H_s, T_p)\) :
- Hauteur significative et période pic par système de houle (décomposition en partitions spectrales)
- Directions dominantes de chaque partition
- Largeur directionnelle (spreading)
- Indicateur de multi-pic (nombre et séparation des systèmes)
- Angle relatif de chaque système par rapport au cap du navire
Ces descripteurs constituent le vecteur d’entrée du modèle de performance.
3.2.2 Calibration du modèle de performance
Les mesures simultanées de vitesse sur l’eau (loch), vitesse fond (GPS), puissance propulsive (couple-mètre ou consommation instantanée) et état de chargement permettent de calibrer la relation :
La calibration peut être formulée comme un problème d’estimation de paramètres (moindres carrés non linéaires) ou d’apprentissage supervisé (forêt aléatoire, réseau de neurones peu profond), selon la quantité de données disponibles et le degré de physique que l’on souhaite conserver dans le modèle.
3.2.3 Boucle de rétroaction
Le modèle calibré évolue dans le temps : chaque voyage fournit de nouvelles observations qui affinent les paramètres. En particulier, la dégradation progressive de la coque par fouling entre deux passages en cale sèche se traduit par une dérive détectable des coefficients de résistance, ce qui fournit un indicateur indirect de l’état de la carène.
L’objectif n’est pas de remplacer les modèles hydrodynamiques établis, mais de les corriger empiriquement pour le navire réel dans ses conditions d’exploitation réelles. Le modèle ainsi calibré alimente ensuite les simulations de consommation sous les différents scénarios météorologiques issus du clustering (section 2).
4. Problème 3 : l’instabilité des trajectoires optimales
4.1 Diagnostic
Même avec un modèle navire calibré et des scénarios météorologiques pertinents, l’optimisation de route reste un problème mal posé au sens où l’espace des trajectoires stochastiques est dépourvu de structure régulière exploitable.
Chaque scénario météorologique produit un champ de coûts différent. La route optimale dans un champ donné n’a, en général, aucune proximité géographique avec la route optimale dans un champ voisin. L’espace des trajets possibles n’est pas un espace vectoriel lisse : c’est un ensemble de chemins aléatoires dans un champ de coûts lui-même aléatoire. La fonction de coût est hautement non convexe, non lisse, avec de multiples minima locaux.
4.2 Échec de l’optimisation de Pareto
Une optimisation multi-objectif de type Pareto (temps vs. carburant vs. risque) dans cet espace produit un front fragmenté : de faibles variations de pondération entre critères entraînent des sauts topologiques importants dans l’espace des routes. Des routes géographiquement très différentes correspondent à des gains marginaux sur un critère. D’une ré-optimisation à l’autre (par exemple toutes les 24 heures), les solutions proposées peuvent être radicalement différentes.
Ces comportements sont incompatibles avec l’exploitation opérationnelle. Le capitaine a besoin d’une route stable, compréhensible, qui évolue de manière prévisible au fil des mises à jour. Le front de Pareto expose des compromis théoriques mais ne fournit pas de base de décision exploitable.
4.3 Approche proposée : splines contraintes à enveloppe exponentielle
Nous proposons d’abandonner la recherche d’un front de Pareto global et de paramétrer la route sous la forme d’une B-spline cubique définie par un nombre réduit de points de contrôle (\(N_c\) = 4 à 8) autour d’une route de référence \(\mathbf{x}_{\text{ref}}(t)\) (route orthodromique ou plan de voyage initial).
Les points de contrôle sont les seules variables d’optimisation. La spline garantit par construction la continuité de courbure (classe \(C^2\)), éliminant les artefacts de zigzag sans recours à des pénalités arbitraires.
4.3.1 Enveloppe à décroissance exponentielle
L’écart latéral maximal à la route de référence est contraint par :
La contrainte s’écrit :
Au début du voyage, la prévision offre un signal exploitable pour dévier de la route directe (contourner une dépression, exploiter un courant). À mesure que l’horizon augmente, l’incertitude croît et la route directe redevient la meilleure référence en l’absence de signal robuste. En fin de voyage, l’information météorologique à longue échéance n’est plus fiable et le couloir se referme : la route directe est la meilleure route.
4.3.2 Propriétés
La combinaison spline + enveloppe élimine les sauts topologiques : l’espace de paramètres est de faible dimension (\(2N_c\) variables) et le couloir borné assure que deux solutions voisines en paramètres sont voisines géographiquement. La ré-optimisation en cours de voyage produit des évolutions progressives de la route, jamais de changement radical.
Le cadre se combine naturellement avec une stratégie de commande prédictive à horizon glissant (MPC) : à chaque cycle, le couloir se réouvre à la position actuelle avec les prévisions mises à jour. En restreignant l’espace de recherche par la géométrie, on revient à un critère scalaire unique (carburant ou temps) pour chaque scénario, sans les artefacts de la fragmentation Pareto.
4.3.3 Calibration
Le paramètre \(\tau\) se calibre empiriquement en comparant l’erreur de prévision en fonction du délai sur un historique ERA5–ECMWF ou ERA5–GFS, par bassin et par saison. Typiquement, \(\tau \approx\) 72–96 heures pour l’Atlantique Nord en hiver. Le nombre de points de contrôle \(N_c\) a une interprétation opérationnelle directe : le nombre de changements de cap significatifs autorisés sur la traversée.
5. Articulation des trois approches
Les trois propositions opèrent dans des espaces différents mais se combinent en un pipeline cohérent.
Le clustering de scénarios (problème 1) structure l’espace des situations météorologiques. Il transforme un continuum de prévisions bruitées en un nombre réduit de situations-types, chacune assortie d’une probabilité. Les simulations de Monte Carlo paramétriques, conditionnelles à chaque cluster, explorent la variabilité intra-scénario et produisent des distributions de variables métocéaniques.
La calibration spectrale (problème 2) produit un modèle de performance fidèle au navire réel. Chaque réalisation Monte Carlo est propagée à travers ce modèle calibré pour produire une distribution de consommation par scénario — non un chiffre, mais un intervalle de confiance.
Les splines contraintes (problème 3) structurent l’espace des routes à l’intérieur de chaque scénario, en produisant des trajectoires lisses, stables et géographiquement réalistes.
Le flux complet s’écrit :
Exemple de sortie opérationnelle
Le navigateur reçoit un tableau de bord structuré :
| Scénario | Probabilité | Consommation (IC 90 %) | ETA | Route |
|---|---|---|---|---|
| A — Dépression passant au nord | 55 % | 430–460 t (méd. 443 t) | +2 h | Déviation sud de 35 NM les 48 premières heures, puis convergence vers le grand cercle |
| B — Dépression passant au sud | 30 % | 460–510 t | +6 h | Maintien du grand cercle, réduction de vitesse à partir de J+2 |
| C — Anticyclone persistant | 15 % | 390–420 t | −3 h | Grand cercle, vitesse économique |
Pour chaque scénario, les hypothèses du modèle, les incertitudes de la prévision et les limites de la calibration sont exposées. Le capitaine arbitre entre les scénarios en fonction de ses propres critères : marge d’ETA, confort de l’équipage, état du navire, consignes de l’armement.
6. Discussion
6.1 Positionnement
Le routage par graphe (VISIR-2 [13], Dijkstra modifié) et par isochrones produit des solutions de qualité mais ne traite ni la sélection de scénarios ni la confiance décroissante dans la prévision. La méthode AnEn est établie en météorologie [12] mais n’a pas, à notre connaissance, été combinée avec une métrique de Wasserstein spatio-temporelle pour le routage maritime. La calibration de modèles hydrodynamiques par données opérationnelles fait l’objet de travaux récents [14] mais reste rarement couplée à l’optimisation de route.
6.2 Limites
Le cadre repose sur l’hypothèse de quasi-ergodicité : les situations passées (ERA5, 1940–2024) sont représentatives des situations futures, conditionnellement à la zone et à la saison. Cette hypothèse est raisonnable à moyen terme mais discutable sous l’effet du changement climatique.
La reconstitution spectrale dépend de la qualité et de la disponibilité des capteurs à bord. Sans radar bande X dédié (type Miros Wavex), la reconstitution repose sur les accéléromètres et inclinomètres, dont la bande passante et la résolution limitent la qualité du spectre directionnel reconstruit.
Le pipeline de sélection d’analogues introduit plusieurs hyperparamètres (taille de la fenêtre, nombre de clusters, seuils) qui nécessitent une validation sur des cas historiques documentés.
6.3 Philosophie d’emploi
Ce cadre n’est pas conçu comme un système d’optimisation automatique. Il est conçu comme un outil d’analyse qui fournit aux navigateurs les moyens de comprendre les situations météorologiques possibles, leurs conséquences sur la consommation et les routes, et les incertitudes associées. L’arbitrage reste humain.
Un système de routage honnête est, avant tout, un système qui montre ce qu’il ne sait pas.
7. Conclusion
Le routage météorologique en marine marchande est confronté à trois problèmes fondamentaux : l’inadéquation des scénarios météorologiques génériques, l’écart entre les modèles de performance et le comportement réel du navire, et l’absence de structure exploitable dans l’espace des trajectoires stochastiques. Ces trois problèmes sont de natures différentes — statistique, physique, mathématique — mais convergent vers une même conséquence : les systèmes de routage actuels produisent des résultats dont la précision apparente masque des incertitudes considérables.
Les approches proposées — clustering d’analogues par distance de Wasserstein, simulations de Monte Carlo paramétriques conditionnelles, calibration spectrale du modèle navire, et splines contraintes à enveloppe exponentielle — ne prétendent pas éliminer ces incertitudes. Elles visent à les structurer, les quantifier et les rendre visibles au décideur.
La conclusion de ce travail est que la meilleure approche du routage météorologique n’est pas d’automatiser la décision de route, mais de fournir aux navigateurs les outils d’analyse nécessaires — scénarios identifiés et probabilisés, modèle de performance calibré sur le navire réel, espace de décision délimité et stable — pour qu’ils effectuent eux-mêmes des arbitrages éclairés. Le rôle de l’algorithme est de structurer l’information, non de se substituer au jugement du capitaine.
Références
- Zis, T.P.V., North, R.J., Angeloudis, P., Ochieng, W.A., and Bell, M.G.H. (2020). “Evaluation of weather routing in reducing fuel consumption and CO2 emissions.” Transportation Research Part D: Transport and Environment, 81:102265.
- Walther, L., Rizvanolli, A., Wendebourg, M., and Jahn, C. (2016). “Modeling and optimization algorithms in ship weather routing.” International Journal of e-Navigation and Maritime Economy, 4:31–45.
- Lu, R., Turan, O., Boulougouris, E., Banks, C., and Incecik, A. (2015). “A semi-empirical ship operational performance prediction model for voyage optimization towards energy efficient shipping.” Ocean Engineering, 110:18–28.
- Bauer, P., Thorpe, A., and Brunet, G. (2015). “The quiet revolution of numerical weather prediction.” Nature, 525(7567):47–55.
- Schultz, M.P. (2007). “Effects of coating roughness and biofouling on ship resistance and powering.” Biofouling, 23(5):331–341.
- Liu, S. and Papanikolaou, A. (2016). “Fast approach to the estimation of the added resistance of ships in head waves.” Ocean Engineering, 112:211–225.
- Holtrop, J. and Mennen, G.G.J. (1982). “An approximate power prediction method.” International Shipbuilding Progress, 29(335):166–170.
- IMO (2012). “Interim Guidelines for the Calculation of the Coefficient fw for Decrease of Ship Speed in a Representative Sea Condition.” MEPC.1/Circ.796 (STAWAVE-1/2).
- Hersbach, H. et al. (2020). “The ERA5 global reanalysis.” Quarterly Journal of the Royal Meteorological Society, 146(730):1999–2049.
- Villani, C. (2009). Optimal Transport: Old and New. Grundlehren der mathematischen Wissenschaften, Vol. 338. Springer-Verlag.
- Cuturi, M. (2013). “Sinkhorn Distances: Lightspeed Computation of Optimal Transport.” Advances in Neural Information Processing Systems, 26:2292–2300.
- Delle Monache, L. et al. (2013). “Probabilistic Weather Prediction with an Analog Ensemble.” Monthly Weather Review, 141(10):3498–3516.
- Mannarini, G., Pinardi, N., Coppini, G., Oddo, P., and Iafrati, A. (2016). “VISIR-I: small vessel — Loss estimates and route optimization.” Journal of Marine Science and Engineering, 4(2):36.
- Nielsen, U.D. (2017). “A concise account of techniques available for shipboard sea state estimation.” Ocean Engineering, 129:352–362.